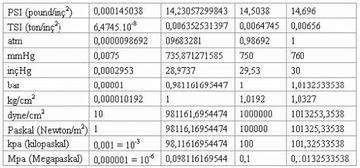
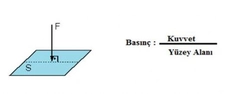
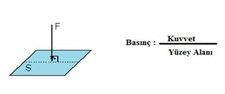
Basınç ve Mol İlişkisi Nedir, Nasıl Hesaplanır?Basınç ve mol ilişkisi, gazların davranışını anlamak için temel bir kavramdır. Bu kavram, gazların fiziksel özellikleri üzerine yapılan araştırmalarda büyük önem taşımaktadır. Gazların, belirli bir sıcaklık ve hacimdeki mol sayısına göre nasıl davrandığını anlamak, mühendislik, kimya, fizik ve çevre bilimleri gibi birçok alanda kritik bir rol oynamaktadır. Basınç Nedir?Basınç, bir yüzeye uygulanan kuvvetin, o yüzeyin alanına bölünmesiyle tanımlanır. Matematiksel olarak basınç, P = F/A formülü ile ifade edilir; burada P basıncı, F kuvveti ve A yüzey alanını temsil eder. Basınç birimi genellikle Pascal (Pa) cinsindendir, ancak atmosfer (atm) ve milimetre cıva (mmHg) gibi diğer birimler de kullanılmaktadır. Molar Hacim ve Molar BasınçMol, bir maddenin birimidir ve Avogadro sayısı (yaklaşık 6.022 x 10²³) kadar birim içeren bir madde miktarını ifade eder. Molar hacim, bir mol gazın belirli bir sıcaklık ve basınç altında kapladığı hacmi tanımlar. Standart koşullar altında (0°C ve 1 atm), bir mol gazın hacmi yaklaşık 22.4 litredir. Basınç ve mol ilişkisini açıklamak için ideal gaz yasası kullanılır. Bu yasa, bir gazın basıncı, hacmi, mol sayısı ve sıcaklığı arasındaki ilişkiyi tanımlayan bir matematiksel ifadedir: PV = nRTBurada,- P = Gazın basıncı- V = Gazın hacmi- n = Gazın mol sayısı- R = Gaz sabiti (8.314 J/(mol·K))- T = Gazın sıcaklığı (Kelvin cinsinden) Bu denklemden yola çıkarak, gazın basıncı ile mol sayısı arasındaki ilişkiyi inceleyebiliriz. Örneğin, sabit sıcaklık ve hacim altında gazın mol sayısını artırdığımızda, basıncın da artacağı görülmektedir. Basınç ve Mol İlişkisinin HesaplanmasıBir gazın basıncını ve mol sayısını hesaplamak için ideal gaz yasasından yararlanabiliriz. Örneğin, 5 mol bir gazın 10 litrelik bir hacimde 300 K sıcaklıkta tutulduğunu varsayalım: 1. Verilen değerleri yerine koyarak hesaplama yapalım: - n = 5 mol - V = 10 L = 0.01 m³ (1 L = 0.001 m³) - R = 8.314 J/(mol·K) - T = 300 K2. İdeal gaz yasasını kullanarak basıncı bulalım: P = nRT/V P = (5 mol) (8.314 J/(mol·K)) (300 K) / (0.01 m³) P = 124,710 Pa veya yaklaşık 124.71 kPa Sonuç olarak, gazın basıncı 124.71 kPa olarak hesaplanmıştır. Bu hesaplama, gazların temel özelliklerini ve davranışlarını anlamada önemli bir rol oynamaktadır. Ekstra BilgilerBasınç ve mol ilişkisi, gazların fiziksel özelliklerini anlamak için kritik bir öneme sahiptir. Bu ilişki, çoğu gaz yasası ve termodinamik prensiplerin temelini oluşturur. Gazların davranışını anlamak, birçok bilim dalında uygulamalara ve araştırmalara yön vermektedir. |
Basınç ve mol ilişkisini öğrenmek oldukça ilginç değil mi? Özellikle gazların davranışını anlamak için bu kavramların ne kadar kritik olduğunu düşündüğümüzde, bu bilgilerin mühendislik ve bilim alanındaki uygulamaları da oldukça geniş. Gazların fiziksel özelliklerini anlamak için ideal gaz yasasının nasıl çalıştığını görmek, bu konudaki ilginç detaylardan biri. Örneğin, belirli bir sıcaklık ve hacim altında gazın mol sayısını artırdığımızda basıncın artacağı gerçeği, birçok uygulamada nasıl bir etki yaratıyor? Bu tür hesaplamalar yaparken, gerçek gazların ideal gaz yasasından sapmalarının da dikkate alınması gerektiğini unutmamak önemli. Sizce bu sapmalar, pratikte ne tür zorluklara yol açabilir?
Cevap yaz