
10. sınıf basınçla ilgili formüller nelerdir?
Bu içerik, 10. sınıf düzeyinde basınçla ilgili temel formülleri ve kavramları açıklamaktadır. Basıncın tanımından başlayarak, sıvılardaki ve gazlardaki basınç hesaplamalarına kadar çeşitli konular ele alınmaktadır. Ayrıca, basıncın günlük yaşamda ve bilimsel uygulamalardaki önemine de vurgu yapılmaktadır.
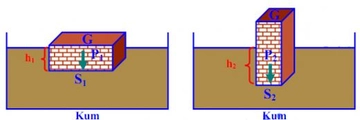
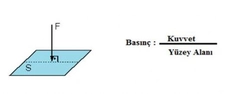
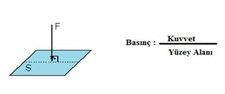
10. Sınıf Basınçla İlgili Formüller Nelerdir?Basınç, birim yüzeye uygulanan kuvvet olarak tanımlanır ve fiziksel olayların anlaşılmasında önemli bir yere sahiptir. Bu makalede, 10. sınıf düzeyinde basınçla ilgili temel formüller ve kavramlar üzerinde durulacaktır. 1. Basınç Tanımı Basınç, bir yüzeye etki eden kuvvetin, o yüzeyin alanına oranı olarak ifade edilir. Matematiksel olarak basınç (P) aşağıdaki formülle gösterilir:
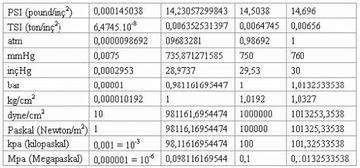
Burada;- P: Basınç (Pascal cinsinden)- F: Kuvvet (Newton cinsinden)- A: Alan (m² cinsinden) 2. Basınç Birimleri Basınç birimleri arasında en yaygın olanları şunlardır:
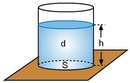
1 Pascal, bir Newton'luk kuvvetin 1 metrekarelik bir alana uyguladığı basıncı ifade eder. Diğer birimler arasında dönüşüm yapılabilir; örneğin, 1 atm = 101325 Pa ve 1 bar = 100000 Pa'dır. 3. Sıvılarda Basınç Sıvılarda basınç, derinlik ile artmaktadır. Sıvı içindeki basınç (P) aşağıdaki formülle hesaplanır:
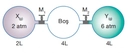
Burada;- ρ: Sıvının yoğunluğu (kg/m³ cinsinden)- g: Yerçekimi ivmesi (9.81 m/s²)- h: Derinlik (m cinsinden) Bu formül, sıvıların derinliğine bağlı olarak basıncın nasıl değiştiğini göstermektedir. 4. Gazlarda Basınç Gazların basıncı, sıcaklık ve hacim ile de ilişkilidir. Bu ilişki, ideal gaz yasası ile açıklanır:
Burada;- P: Gazın basıncı (Pa)- V: Gazın hacmi (m³)- n: Mol sayısı- R: Gaz sabiti (8.314 J/(mol·K))- T: Sıcaklık (Kelvin cinsinden) Bu formül, gazların davranışlarını anlamak için temel bir araçtır. 5. Uygulama Alanları Basınç, birçok bilimsel ve mühendislik uygulamasında kritik bir rol oynar. Bazı örnekler:
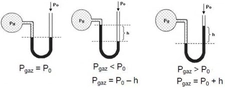
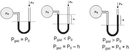
Bu uygulamalar, basıncın nasıl çalıştığını ve günlük yaşamda ne kadar önemli olduğunu göstermektedir. Ekstra Bilgiler - Basınç, fiziksel olayların yanı sıra biyolojik sistemlerde de önemlidir. Örneğin, insan vücudundaki kan basıncı, sağlığın bir göstergesi olarak kabul edilir.- Basınç ölçümü için kullanılan aletler arasında manometreler ve barometreler bulunmaktadır. Sonuç olarak, basınç, doğanın temel bir özelliği olup, birçok farklı alanda uygulama bulmaktadır. 10. sınıf düzeyinde öğrenilen bu formüller, öğrencilerin fiziksel olayları anlamalarına yardımcı olur ve daha karmaşık konulara geçiş yapmalarını kolaylaştırır. Bu nedenle, basınçla ilgili kavramların ve formüllerin iyi bir şekilde kavranması büyük önem taşımaktadır. |


















Basınçla ilgili formülleri öğrenmek gerçekten önemli bir konu değil mi? Özellikle P = F / A formülü üzerinden basıncın tanımını anlamak, fiziksel olayları kavramamızda büyük bir katkı sağlıyor. Sıvılardaki basıncın derinlikle artması ve P = ρgh formülü, su altında neler olduğunu anlamamızda oldukça faydalı. Gazlar için ise PV = nRT formülü, sıcaklık ve hacimle basınç arasındaki ilişkiyi net bir şekilde gösteriyor. Bu formülleri günlük yaşamda nasıl gözlemlediğinizi merak ediyorum. Örneğin, su pompaları veya meteorolojik ölçümler sırasında bu bilgilerin nasıl uygulandığını düşündünüz mü?
Basınç Formüllerinin Önemi
ÇeŞman, basınç formüllerini öğrenmek gerçekten de önemli bir konu. Basıncın tanımını anlamak, fiziksel olayları kavramamıza büyük katkı sağlıyor. Özellikle P = F / A formülü, kuvvetin yüzeye etki eden etkisini net bir şekilde gösteriyor. Bu da çeşitli alanlarda, günlük yaşamda karşılaştığımız birçok durumu anlamamıza yardımcı oluyor.
Sıvılardaki Basınç ve Derinlik
Sıvılardaki basıncın derinlikle artması ve P = ρgh formülü, su altındaki basınç değişimlerini anlamamızı sağlıyor. Örneğin, bir dalgıç suya daldığında, derinliğe bağlı olarak basıncın artması, vücut üzerindeki etkilerini gösteriyor. Bu tür bilgilerin farkında olmak, su altında güvenli bir şekilde hareket etmeyi sağlıyor.
Gazların Davranışı
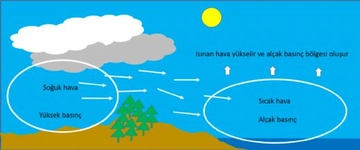
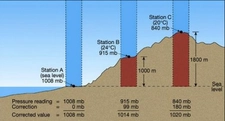
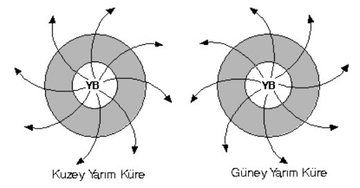
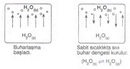
Gazlar için PV = nRT formülü de sıcaklık ve hacimle basınç arasındaki ilişkiyi anlamamıza yardımcı oluyor. Gazların davranışını gözlemlemek, örneğin bir balonun sıcaklık arttıkça genişlemesi gibi günlük hayatta sıkça karşılaştığımız durumlarda önemli. Meteorolojik ölçümlerde ise havanın basıncının değişimi, hava durumu tahminlerinde büyük rol oynuyor.
Sonuç olarak, bu formüllerin günlük yaşamdaki uygulamalarını gözlemlemek, fiziksel olayları daha iyi anlamamıza ve bu bilgileri pratikte nasıl kullanabileceğimizi görmemize yardımcı oluyor. Bu tür bilgiler, bilimsel düşünme becerimizi geliştiriyor ve çevremizdeki dünyayı daha iyi kavramamıza olanak tanıyor.